Post

Flare-On 11 Write-Up Part 1

Posted
By Victor de Pedraza Ajenjo
10 min read
Flare-On 11 Write-Up Part 1

Over the past few weeks, I took part in the eleventh FLARE-ON Reverse Engineering Capture-the-Flag (CTF) competition.

I managed to solve 6 out of the 10 challenges in this year’s Flare-On, picking up some great experience and learning more about Reverse Engineering along the way. The competition was tough but fun, and I’m already looking forward to next year’s event.

In this post, I’ll share my write-ups for the challenges I solved. One thing I love about this CTF is its linear format, which helps you stay focused by letting you work on one challenge at a time.

You can also find supplementary resources, including the scripts I used throughout the CTF, in this repository.

Challenge 1 - frog

Your mission is get the frog to the “11” statue, and the game will display the flag. Enter the flag on this page to advance to the next stage.

This was the first challenge in the Flare-On 11 competition, and it served as a warm-up. It introduced a simple problem that could be solved by analyzing Python code. Let’s break it down step by step.

We were provided with a small game written in Python using the PyGame library, along with its source code. The goal was to reverse engineer the program and extract the hidden flag.

Step 1: Understanding the Code

Upon opening the main game file, I skimmed through the source code and noticed a function named GenerateFlagText. This function appeared to generate the flag using some form of encoding and two coordinates passed as arguments. Here’s the function:

1
2
3
4

def GenerateFlagText(x, y):
    key = x + y*20
    encoded = "\xa5\xb7\xbe\xb1\xbd\xbf\xb7\x8d\xa6\xbd\x8d\xe3\xe3\x92\xb4\xbe\xb3\xa0\xb7\xff\xbd\xbc\xfc\xb1\xbd\xbf"
    return ''.join([chr(ord(c) ^ key) for c in encoded])

Step 2: Identifying Where It’s Used

I noticed that this function is called in the game’s main loop when the player coordinates matches the victory_tile coordinates:

1
2
3
4
5
6

if player.x == victory_tile.x and player.y == victory_tile.y:
    victory_mode = True
    flag_text = GenerateFlagText(player.x, player.y)
    flag_text_surface = flagfont.render(flag_text, False, pygame.Color('black'))
    print("%s" % flag_text)

The victory_tile coordinates are defined at the beginning of the file:

1

victory_tile = pygame.Vector2(10, 10)

Step 3: Extracting the Flag

Now that we know that the tile coordinates are (10, 10), we can calculate the key and decode the flag without even running the game.

I opened a Python interpreter and executed the GenerateFlagText function directly, obtaining the first flag:

1
2
3
4
5
6
7
8

$ python3
>>> def GenerateFlagText(x, y):
...     key = x + y*20
...     encoded = "\xa5\xb7\xbe\xb1\xbd\xbf\xb7\x8d\xa6\xbd\x8d\xe3\xe3\x92\xb4\xbe\xb3\xa0\xb7\xff\xbd\xbc\xfc\xb1\xbd\xbf"
...     return ''.join([chr(ord(c) ^ key) for c in encoded])
...
>>> GenerateFlagText(10, 10)
'welcome_to_11@flare-on.com'

Challenge 2 - checksum

We recently came across a silly executable that appears benign. It just asks us to do some math… From the strings found in the sample, we suspect there are more to the sample than what we are seeing. Please investigate and let us know what you find!

Now the real challenges begin! For this task, we were given a single file to analyze: checksum.exe.

Step 1: Initial analysis

As an initial step, I ran the strings command on the binary, which revealed a number of references to GoLang. Loading the binary into Ghidra confirmed it was a Go binary, and the tool identified it as such.

Running the executable on a Windows machine revealed a CLI that required solving arithmetic problems. After several calculations, the program requested a “Checksum” that we needed to determine:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

C:\Users\pumuki\Desktop+>checksum.exe
Check sum: 8322 + 3603 = 11925
Good math!!!
------------------------------
Check sum: 3990 + 1309 = 5299
Good math!!!
------------------------------
Check sum: 8346 + 4096 = 12442
Good math!!!
------------------------------
Check sum: 2683 + 5878 = 8561
Good math!!!
------------------------------
Check sum: 6050 + 3440 = 9490
Good math!!!
------------------------------
Check sum: 8028 + 7421 = 15449
Good math!!!
------------------------------
Checksum: hello
Not a valid checksum...

FLARE 24/11/2024  0:09:05,42
C:\Users\pumuki\Desktop+>

Step 2: Static analysis

After loading the binary into Ghidra, I began by inspecting the main.main symbol, which serves as the program’s entry point. This function was quite large and seemed to encompass most of the program’s logic.

I identified function calls and strings that matched the program’s output, the “Good math!!!” message from earlier was clearly visible in the decompiled code:

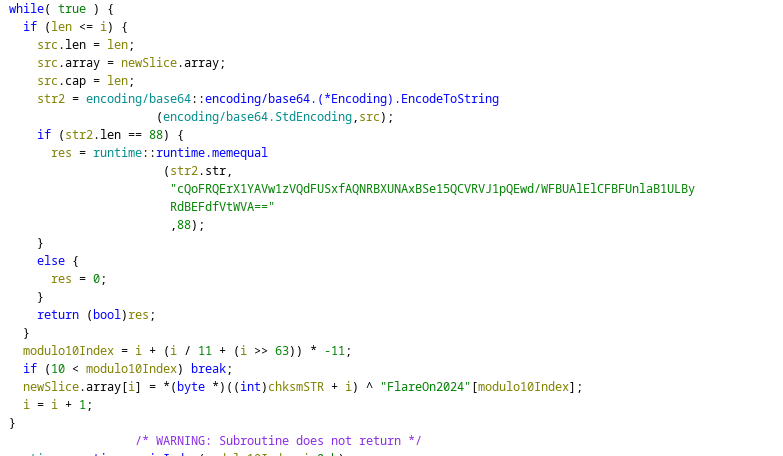
img-description

After a bit of effort I recognised the while loop that asked for the Check Sums. This loop iterated between 3 and 8 times:

img-description

At this point, I realized the “Check sum” inputs were unrelated to the final checksum verification. Instead, the provided checksum was validated by a function, which then generated a ChaCha20 key to decrypt the file REAL_FLAREON_FLAG.JPG.

Step 3: Checksum algorithm

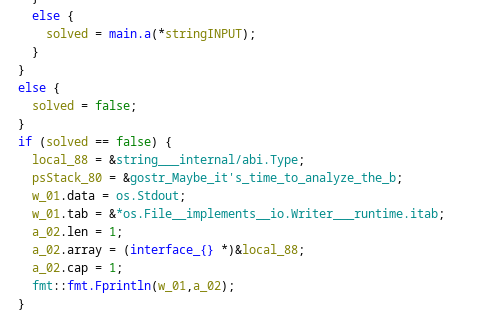
The validation function (main.a) stood out. It took the provided checksum as input and returned a boolean, printing an error message if the checksum was invalid:

img-description

This function gave me a little headeache because of how it was structured. Inside main.a, the checksum validation logic worked as follows:

  1. Xor the provided string with the FlareOn2024 string
  2. When all bytes have been xored if (len <= i):
    1. Encode to base64
    2. Check that the length is equal to 88
    3. Check that the base64 encoded data is equal to cQoFRQErX1YAVw1zVQdFUSxfAQNRBXUNAxBSe15QCVRVJ1pQEwd/WFBUAlElCFBFUnlaB1ULByRdBEFdfVtWVA==

With this knowledge, I wrote a script to reverse these steps and calculate the required checksum.

img-description

Step 4: Solving

Here’s the Python script I wrote to reverse the checksum algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import base64
import itertools

def xor_bytes(byte_string, xor_key):
    # Use itertools.cycle to repeat the xor_key as needed
    repeated_key = itertools.cycle(xor_key)
    x = list((a ^b) for a, b in zip(byte_string, repeated_key))
    return bytes(x)

# Hardcoded Base64 string
base64_string = "cQoFRQErX1YAVw1zVQdFUSxfAQNRBXUNAxBSe15QCVRVJ1pQEwd/WFBUAlElCFBFUnlaB1ULByRdBEFdfVtWVA=="

# Decode the Base64 string to get the original bytes
decoded_bytes = base64.b64decode(base64_string)
print(len(decoded_bytes))

# Another byte string to XOR with
xor_key = b"FlareOn2024"

# Perform XOR
xor_result = xor_bytes(decoded_bytes, xor_key)

# Print the XOR result
print(xor_result)

After running the script, I provided the checksum to the program:

1
2
3
4
5
6
7
8
9
10
11
12

C:\Users\pumuki\Desktop+>checksum.exe
Check sum: 8322 + 3603 = 11925
Good math!!!
------------------------------
Check sum: 3990 + 1309 = 5299
Good math!!!
------------------------------
Check sum: 8346 + 4096 = 12442
Good math!!!
------------------------------
Checksum: 7fd7dd1d0e959f74c133c13abb740b9faa61ab06bd0ecd177645e93b1e3825dd
Noice!!

The program successfully decrypted the file REAL_FLAREON_FLAG.JPG, which was saved in %LOCALAPPDATA%:

img-description

Challenge 3 - aray

And now for something completely different. I’m pretty sure you know how to write Yara rules, but can you reverse them?

In this challenge, we were given a YARA rule to reverse engineer. YARA is a powerful pattern-matching tool commonly used to create malware signatures. Our goal was to find the file that satisfies all the conditions in the provided YARA rule.

1
2
3
4
5
6
7

cat aray.yara | head -c 300
rule aray
{
    meta:
        description = "Matches on b7dc94ca98aa58dabb5404541c812db2"
    condition:
        filesize == 85 and hash.md5(0, filesize) == "b7dc94ca98aa58dabb5404541c812db2" and filesize ^ uint8(11) != 107 and uint8(55) & 128 == 0 and uint8(58) + 25 == 122 and uint8(

Step 1: Initial Analysis

This YARA rule contained several conditions, all of which had to match. Two initial conditions defined the file size and MD5 hash:

  • filesize == 85
  • hash.md5(0, filesize) == "b7dc94ca98aa58dabb5404541c812db2"

Next, it included numerous byte-level conditions like:

  • Exact matches: uint8(84) + 3 == 128
  • Comparisons: uint8(20) < 135

To solve this challenge, I set the exact-match bytes first and then used brute-forcing to determine the remaining bytes.

Step 2: Parsing the Rule

I wrote a simple script to identify and parse the rules which produced exact matches:

1
2
3
4
5
6

rule = 'filesize == 85 and hash.md5(0, filesize) == "b7dc94c' ...

ruleList = rule.split("and")
for r in ruleList:
    if "==" in r and not "&" in r:
        print(r)

This script helped categorize the conditions into the following groups:

  • Hash Conditions:
    • hash.sha256(pos, 2) == val defines 2 bytes and appears 4 times
    • hash.md5(pos, 2) == val defines 2 bytes and appears 2 times
    • hash.crc32(pos, 2) == val defines 2 bytes and appears 4 times
  • Byte Constraints:
    • uint8(pos) + val1 == val2 defines 1 bytes and appears 13 times
    • uint32(pos) ^ val1 == val2 defines 4 bytes and appears 13 times

Step 3: Determining Byte Values

Hash Constraints

For hash-based conditions, I used online tools, like this one to find the corresponding byte values:

1
2
3
4
5
6
7

 hash.md5(0, 2) == "89484b14b36a8d5329426a3d944d2983" -> "ru"
 hash.md5(76, 2) == "f98ed07a4d5f50f7de1410d905f1477f"  -> "io"
 hash.md5(50, 2) == "657dae0913ee12be6fb2a6f687aae1c7"  -> "3A"
 hash.md5(32, 2) == "738a656e8e8ec272ca17cd51e12f558b"  -> "ul"

 hash.sha256(14, 2) == "403d5f23d149670348b147a15eeb7010914701a7e99aad2e43f90cfa0325c76f"  -> " s"
 hash.sha256(56, 2) == "593f2d04aab251f60c9e4b8bbc1e05a34e920980ec08351a18459b2bc7dbf2f6"  -> "fl"

CRC32 Constraints

For the crc32 conditions I wrote the following script to find the original bytes:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

import zlib
import itertools
import string


def generate_crc32_for_2char_strings():
    # Generate all possible 2-character strings (from printable ASCII characters)
    chars = string.printable  # Printable ASCII characters
    combinations = itertools.product(chars, repeat=2)

    # Iterate through each combination and compute its CRC32
    for combination in combinations:
        input_string = ''.join(combination)
        crc_value = zlib.crc32(input_string.encode())

        yield (input_string, crc_value)


# Run the function
generate_crc32_for_2char_strings()

for input, crc32 in generate_crc32_for_2char_strings():
    if crc32 == 0x61089c5c:
        print(hex(crc32), input)
    if crc32 == 0x5888fc1b:
        print(hex(crc32), input)

    if crc32 == 0x66715919:
        print(hex(crc32), input)

    if crc32 == 0x7cab8d64:
        print(hex(crc32), input)

1
2
3
4

 hash.crc32(8, 2) == 0x61089c5c  -> "re"
 hash.crc32(34, 2) == 0x5888fc1b  -> "eA"
 hash.crc32(63, 2) == 0x66715919  -> "n."
 hash.crc32(78, 2) == 0x7cab8d64  -> "n:"

Byte Level Constraints

For the uint8 and uint32 constraints, I solved them using a calculator. Examples:

1
2
3
4
5
6

 uint8(58) + 25 == 122 -> "a"
 uint32(52) ^ 425706662 == 1495724241 -> "w4y@" 
 uint32(17) - 323157430 == 1412131772  -> "ring"
 uint8(36) + 4 == 72 -> "D"
 uint8(27) ^ 21 == 40 -> "="
 ...

Building the File

Once I identified these values, I populated them into a byte array. Here’s a snippet of the script I used to assemble the file. Complete script:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

with open("out.txt","wb") as outputFD:
    outputBuffer = bytearray(b"")
    outputBuffer += bytearray(b"_"*85)

    # hash.md5 checks define:
    outputBuffer[50] = ord("3")
    outputBuffer[51] = ord("A")

    ...

    # bitwise on basic operations
    outputBuffer[52] = 119
    outputBuffer[53] = 52
    outputBuffer[54] = 121
    outputBuffer[55] = 64

    outputBuffer[17] = 114
    outputBuffer[18] = 105
    outputBuffer[19] = 110
    outputBuffer[20] = 103

    ...

    # sha256 rules
    outputBuffer[14] = ord(" ")
    outputBuffer[15] = ord("s")

    ..

    # write solution

    if len(outputBuffer) != 85:
        print("ERROR, INCORRECT OUTPUT LENGTH")
        exit(-1)
    outputFD.write(outputBuffer)

This gives us the following output, we have found all characters: rule flareon { strings: $f = "1RuleADayK33p$Malw4r3Aw4y@flare-on.com" condition: $f }

Extra: Brute-forcing with Hashcat

If we hadn’t found all the characters, I could have used Hashcat to brute-force the remaining ones.

In the following example, some characters have been replaced with ?1 to bruteforce them. This allows me to test combinations for specific unknown characters efficiently. With my current setup, I can bruteforce up to 6 characters almost instantly. Here’s a breakdown of the bruteforce speeds:

  • 6 characters: ~3 minutes
  • 7 characters: ~4 hours
  • 8 characters: ~18 days
1
2

echo "b7dc94ca98aa58dabb5404541c812db2" > hash.txt
hashcat -m 0 -a 3 hash.txt 'rule flareon { strings: $f = "1RuleADayK33p$Malw4r3Aw4y@flare-on.?1om" cond?1?1ion: $f ?1' -1 ?l?u?d?s

This approach founds the mathing string:

1

b7dc94ca98aa58dabb5404541c812db2:$HEX[72756c6520666c6172656f6e207b20737472696e67733a202466203d20223152756c65414461794b333370244d616c773472334177347940666c6172652d6f6e2e636f6d2220636f6e646974696f6e3a202466207d]

Decoding the result:

1
2

echo 72756c6520666c6172656f6e207b20737472696e67733a202466203d20223152756c65414461794b333370244d616c773472334177347940666c6172652d6f6e2e636f6d2220636f6e646974696f6e3a202466207d | xxd -r -p
rule flareon { strings: $f = "1RuleADayK33p$Malw4r3Aw4y@flare-on.com" condition: $f }

Continuation

Check the following post here

Hacking, Software
hacking software capture the flag write-up golang reverse engineering
This post is licensed under CC BY 4.0 by the author.